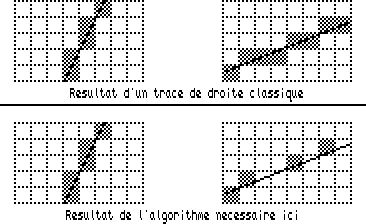La 3D
 Cette rubrique a pour but de vous présenter les bases théoriques de la 3D ainsi que les techniques et astuces d'implémentation sur CPC compte tenu des contraintes du Z80 et de l'architecture vidéo.
Cette rubrique a pour but de vous présenter les bases théoriques de la 3D ainsi que les techniques et astuces d'implémentation sur CPC compte tenu des contraintes du Z80 et de l'architecture vidéo.
Mise en bouche
— Basé sur l'article publié dans Quasar CPC numéro 11, Demomaking, par ATC.
Quand on voit les démos qui sortent sur les autres machines, on peut se demander pourquoi on ne pourrait pas en faire autant sur CPC… D'accord, y'a le petit blond qu'a encore un problème : “y'aura jamais assez de temps machine pour les calculs !” Jusque là, on est d'accord, mais pourquoi est-ce qu'on ne pré-calculerait pas ce qui bouffe le plus de NOP ?
En fait, je vais déjà faire une approche de la programmation d'objets 3D, afin que tout le monde puisse suivre la suite du cours.
La théorie
Avant d'afficher n'importe quel objet, il y a trois étapes importantes à ne pas oublier.
Dans l'ordre :
- on calculera les translations,
- on calculera les rotations,
- on projettera les points 3D sur l'écran 2D.
Prenons un objet 3D constitué de points. Chaque point possède un groupe de trois coordonnées : x, y, z (jusque là, tout le monde suit, et c'est très bien !). La translation sur un axe s'obtient tout simplement en ajoutant la longueur de celle-ci à la coordonnée du point sur cet axe. Euh, bon ! En clair, ça veut dire que pour une translation en X, de 2 unités, on aura le nouveau point X'=X+2. Simple non ?
Maintenant, en ce qui concerne les rotations, les formules vont un peu se compliquer, mais encore rien de bien féroce… Allez, je ne vais pas m'éterniser sur ces formules car cela n'en vaut pas la peine (si vous voulez une démonstration mathématique de ces résultats, vous en trouverez des tas sur l'internet).
 Donc, pour une rotation autour de l'axe x, on a :
Donc, pour une rotation autour de l'axe x, on a :
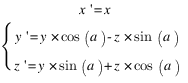
Autour de l'axe y, on aura :
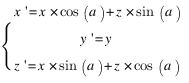
Autour de l'axe z, maintenant :
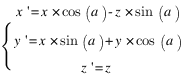
Voilà, à présent, tout le monde doit être capable de faire tourner un objet 3D… en théorie ! Mais maintenant, pourquoi ne pas passer à la pratique ?
La pratique
Pour coder ce genre de choses, vous vous imaginez bien que l'on ne va pas faire un bel écran overscan, avec un beau raster qui bouffe la moitié du temps machine. Non, en fait pour commencer, nous allons nous contenter du simple écran standard du CPC (On verra pour l'overscan une autre fois, mais, bon, si vous voulez voir ce que ça donne, matez une partie 3D de Face Hugger ou encore d'Alien dans Voyage 93).
Pour faire de la 3D sur CPC, le mode qui reste le plus adéquat est encore le mode 0. En effet, lorsque l'on va afficher nos points 3D, nous allons avoir des points de coordonées (x,y), et en mode 0, comme un octet est constitué de deux pixels, on n'aura qu'un masque à faire lors du traçage de lignes, vous avez deux fois moins de points à calculer qu'en mode 1. Mais nous étudierons plus en avant ces aspects lorsque nous nous pencherons sur l'implémentation en assembleur.
Maintenant, un problème se pose : “Comment est-ce que l'on va structurer le programme pour faire tenir tout ça dans une frame ?” Eh bien pour les translations, rien ne change, il ne s'agit en fait que trois simples additions. Mais en ce qui concerne les rotations, c'est une autre histoire !
 En fait, le problème se résout très facilement grâce à un objet mathématique appelé matrice. En effet, lorsque vous calculez vos rotations, pour chaque point, vous devez effectuer trois calculs de suite : les rotations autour des trois axes. À chaque équation écrite ci-dessus correspond une matrice. Allez, je vous les donne sans plus tarder :
En fait, le problème se résout très facilement grâce à un objet mathématique appelé matrice. En effet, lorsque vous calculez vos rotations, pour chaque point, vous devez effectuer trois calculs de suite : les rotations autour des trois axes. À chaque équation écrite ci-dessus correspond une matrice. Allez, je vous les donne sans plus tarder :
Matrice de rotation autour de l'axe x :
![delim{[}
{matrix{3}{3}
{
{1} {0} {0}
{0} {cos(a)} {-sin(a)}
{0} {sin(a)} {cos(a)}
}}
{]} delim{[}
{matrix{3}{3}
{
{1} {0} {0}
{0} {cos(a)} {-sin(a)}
{0} {sin(a)} {cos(a)}
}}
{]}](http://quasar.cpcscene.net/lib/exe/fetch.php?w=&h=&cache=cache&media=cache_mathplugin%3amath_962.5_32d5fdbd84bd8ed4726eb63a37860a81.png)
Matrice de rotation autour de l'axe y :
![delim{[}
{matrix{3}{3}
{
{cos(a)} {0} {sin(a)}
{0} {1} {0}
{-sin(a)} {0} {cos(a)}
}}
{]} delim{[}
{matrix{3}{3}
{
{cos(a)} {0} {sin(a)}
{0} {1} {0}
{-sin(a)} {0} {cos(a)}
}}
{]}](http://quasar.cpcscene.net/lib/exe/fetch.php?w=&h=&cache=cache&media=cache_mathplugin%3amath_962.5_8739e0276eefd927ffd03dc5d27b31bb.png)
Matrice de rotation autour de l'axe z :
![delim{[}
{matrix{3}{3}
{
{cos(a)} {sin(a)} {0}
{sin(a)} {cos(a)} {0}
{0} {0} {1}
}}
{]} delim{[}
{matrix{3}{3}
{
{cos(a)} {sin(a)} {0}
{sin(a)} {cos(a)} {0}
{0} {0} {1}
}}
{]}](http://quasar.cpcscene.net/lib/exe/fetch.php?w=&h=&cache=cache&media=cache_mathplugin%3amath_962.5_745bedaaac25cefab29238e4d35645f7.png)
Mais bon, où est-ce que je veux en venir ? Eh bien c'est très simple. Pourquoi, au lieu d'avoir trois matrices, ne pas en n'avoir qu'une seule qui nous servirait une fois pour chaque point ? Pour ce faire, il ne suffit que de multiplier les trois matrices de rotation simples entre elles. En fait là, ce n'est plus une question de code, mais de maths ; donc si vous ne comprenez pas, révisez vos cours de maths du lycée !
Voici donc notre matrice globale :
![delim{[}
{matrix{3}{3}
{
{cos(b)*cos(c)} {-cos(a)*sin(c)+sin(a)*sin(b)*cos(c)} {sin(a)*sin(c)+cos(a)*sin(b)*cos(c)}
{cos(b)*sin(c)} {cos(a)*cos(c)+sin(a)*sin(b)*sin(c)} {-sin(a)*cos(c)+cos(a)*sin(b)*sin(c)}
{-sin(b)} {sin(a)*cos(b)} {cos(a)*cos(b)}
}}
{]} delim{[}
{matrix{3}{3}
{
{cos(b)*cos(c)} {-cos(a)*sin(c)+sin(a)*sin(b)*cos(c)} {sin(a)*sin(c)+cos(a)*sin(b)*cos(c)}
{cos(b)*sin(c)} {cos(a)*cos(c)+sin(a)*sin(b)*sin(c)} {-sin(a)*cos(c)+cos(a)*sin(b)*sin(c)}
{-sin(b)} {sin(a)*cos(b)} {cos(a)*cos(b)}
}}
{]}](http://quasar.cpcscene.net/lib/exe/fetch.php?w=&h=&cache=cache&media=cache_mathplugin%3amath_961.5_107334158d46414d95b9eb7aa88cdb0c.png)
a, b et c étant respectivement les angles de rotation autour des axes Ox, Oy et Oz (O étant l'origine)
Et voici la façon de s'en servir :
![delim{[}{matrix{3}{3}{A B C D E F G H I}}{]} . delim{[}{matrix{3}{1}{x y z}}{]} = {lbrace}{matrix{3}{1}{{x prime = Ax + By + Cz} {y prime = Dx + Ey + Fz} {z prime = Gx + Hy + Cz}}} delim{[}{matrix{3}{3}{A B C D E F G H I}}{]} . delim{[}{matrix{3}{1}{x y z}}{]} = {lbrace}{matrix{3}{1}{{x prime = Ax + By + Cz} {y prime = Dx + Ey + Fz} {z prime = Gx + Hy + Cz}}}](http://quasar.cpcscene.net/lib/exe/fetch.php?w=&h=&cache=cache&media=cache_mathplugin%3amath_968.5_8fb75050676bbae980cb82bae0f41d26.png)
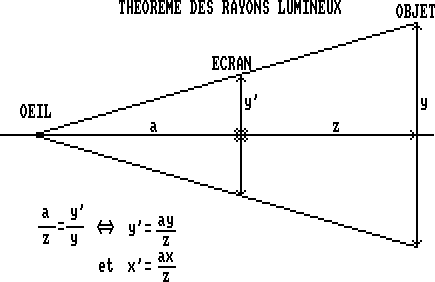
Comme vous savez maintenant calculer les translations et les rotations, il ne vous reste plus qu'à projeter les points 3D sur l'écran. En fait, tout réside dans le théorème des rayons lumineux (vous voyez que ça sert parfois la physique !). Bon, comme ce n'est pas très compliqué, je vais vous filer le schéma ainsi que les formules qui permettent la projection :
Voilà, j'ai encore quelques petites choses à dire à ceux qui ne savent pas comment calculer un sinus ou un cosinus en assembleur. Il faut vous munir d'une table dans laquelles vous mettrez par exemple les valeurs du sinus suivie de celles du cosinus, ces valeurs ayant ét multipliées auparavant (un conseil : par un multiple de deux, ça vous posera moins de problèmes dans le code.). Mais nous reviendrons également sur cet aspect lors de l'étude de l'implémentation en assembleur un peu plus bas.
Mise en programme
— Basé sur l'article publié dans Quasar CPC numéro 13, Assembleur : Coding, par OffseT.
 Après la présentation des aspects théoriques par ATC, nous allons à présent nous intéresser à la mise en pratique à l'aide d'un petit programme en BASIC. Ça y est, c'est parti, le petit blond à lunettes recommence à critiquer… Oui, c'est un programme BASIC, et non, il n'est pas optimisé du tout ! J'ai écrit ce programme de telle sorte qu'il soit compréhensible par le commun des mortels en délimitant au maximum les différentes étapes.
Après la présentation des aspects théoriques par ATC, nous allons à présent nous intéresser à la mise en pratique à l'aide d'un petit programme en BASIC. Ça y est, c'est parti, le petit blond à lunettes recommence à critiquer… Oui, c'est un programme BASIC, et non, il n'est pas optimisé du tout ! J'ai écrit ce programme de telle sorte qu'il soit compréhensible par le commun des mortels en délimitant au maximum les différentes étapes.
Définissons l'objets
La première chose à faire est de définir l'objet 3D. Celui-ci est défini par points dans les DATA des lignes 910 à 930. Dans notre exemple nous définissons les 8 sommets d'un cube. Ces DATA sont mémorisés dans un tableau pour la suite des événements (cf. lignes 160 à 390). Ensuite, on a la ligne 940 dans laquelle on trouve les DATA qui définissent les arêtes de notre cube. La séquence 1,2,3,4,0 signifie : relier le point 1 au point 2, le 2 au 3, le 3 au 4 et stop. Ces DATA sont utilisés lors de l'affichage dans les lignes 850 à 870.
La projection
Deux fonctions sont définies à cet effet. Il s'agit de FNprojx et FNprojy qui renvoient les coordonnées projetées en X et Y du point numéro v. 3, 2, 1, paf ! Le petit blond à lunettes a sorti sa question sournoise : “c'est quoi tx, ty, vx, vy, vz, mag et le 500 ?” Alors, tx et ty dont les positions en x et en y de notre objet dans l'espace. 500, qui est une constante dans mon programme mais que j'aurais aussi bien pu appeler tz est la position en z de l'objet. Ces coordonnées sont à voir par rapport à une origine situées au centre de l'écran avec l'axe X qui part vers la droite, Y vers le haut et Z vers l'arrière de l'écran. En ce qui concerne mag, il s'agit de la position de l'observateur par rapport à l'écran. Je ne reviendrai pas dessus, le sujet a déjà été évoqué par ATC dans la section précédente… Quant aux petits vx, vy et vz, il s'agit de nos tableaux des coordonnées des points de l'objet après calculs de rotation.
Les rotations
Elles sont ici différenciées en x, y et z. Les tableaux px, py et pz contiennent les coordonnées en x, y et z des points de notre objet de départ. Les tableaux tx, ty et tz (à ne pas confondre avec les variables du même nom utilisées dans la projection) sont les nouvelles coordonnées après rotation en x. ux, uy et uz sont les résultats après rotation en y et vx, vy et vz, utilisées dans la projection, contiennent le résultat final après les trois rotations. La variable a, ici commune à toutes les rotations, est l'angle courant de rotation de l'objet par rapport à la position initiale.
Le programme principal
Celcui-ci est d'une simplicité enfantine… On commence par afficher l'objet courant. On incrémente ensuite l'angle de rotation puis on modifie la position x, y (ici on parcours un cercle de rayon 100). On appelle les routines de rotation en x, y et z, puis on boucle. Libre à vous de rendre la position z de l'objet paramétrable ou encore de rendre les rotations indépendantes.
L'affichage
Avant d'afficher bêtement notre objet, il va falloir trier les arêtes. Pour ce faire, on parcours les DATA de la ligne 940. On stocke notre première série dans le tableau a (rien à voir avec la variable a !). On se place ensuite sur le premier point par un MOVE et on fait des DRAW jusqu'aux autres… Rien de bien sorcier.
Les extensions
On peut bien entendu largement optimiser ce programme en terme de temps machine, mais là n'est pas le débat. On peut passer en face pleine… Comment ? Simplement en complétant les séquences raccourcies dans les DATA de la ligne 940 de façon à ne définir que des faces et plus d'arêtes seules. Ensuite, il suffit de calculer le barycentre de chaque face et d'afficher celles-ci de la plus éloignée à la plus proche en les remplissant…
Les ragots
Je vais profiter de cette rubrique pour mettre un terme aux commérages relatifs à la fausse 3D… Je sens en effet que certains vont encore me dire que mon programme est de la fausse 3D… Mais bien sûr que ça en est !!! Jusqu'à preuve du contraire le moniteur du CPC est uniquement capable de reproduire des images en 2D, donc, représenter des objets en 3D sur de la 2D n'est pour ainsi dire pas de la 3D… Pourtant la représentation qui est utilisée ici est la plus performante et si les objets vous semblent déformés c'est uniquement que vos paramètres mag et 500 dans les fonctions de projection ne sont pas bien ajustés ! Pour avoir de bons résultats, je vous conseille d'avoir mag égal à la moitié de la position z de l'objet. Alors, ne venez plus me parler de vraie ou fausse 3D !
Listing : manipulation d'un objet 3D
10 ' Calculs de 3D 20 ' 30 DEFINT a-z 40 ' 50 ' Initialisation des fonctions de projection 60 ' 70 DEF FNprojx(v)=mag*(vx(v)+tx)/(vz(v)+500) 80 DEF FNprojy(v)=mag*(vy(v)+ty)/(vz(v)+500) 90 ' 100 ' Initialisation de l'{cran 110 ' 120 MODE 2 130 ORIGIN 320,200 140 ' 150 DEG 160 ' 170 ' Initialisation de l'objet 180 ' 190 ' Recherche de la taille 200 ' 210 x=0 220 RESTORE 230 x=x+1 240 READ px,py,pz 250 IF px=255 AND py=255 AND pz=255 THEN 260 ELSE 230 260 n=x-1 ' n=nombre de points 270 ' 280 ' Initialisation des tableaux de l'objet 290 ' 300 DIM px(n),py(n),pz(n),vx(n),vy(n),vz(n),a(n) 310 DIM tx(n),ty(n),tz(n),ux(n),uy(n),uz(n) 320 ' 330 ' Lecture de l'objet 340 ' 350 RESTORE 360 FOR x=1 TO n 370 READ px(x),py(x),pz(x) 380 vx(x)=px(x):vy(x)=py(x):vz(x)=pz(x) 390 NEXT 400 ' 410 ' Valeurs initiales 420 ' 430 a=0:mag=256 440 ' 450 ' Programme principal 460 ' 470 WHILE 1 480 GOSUB 850 490 a=(a+10) MOD 360 500 tx=100*SIN(a) 510 ty=100*COS(a) 520 GOSUB 610 530 GOSUB 690 540 GOSUB 770 550 CLG 560 WEND 570 END 580 ' 590 ' Rotation x 600 ' 610 FOR x=1 TO n 620 tx(x)=px(x) 630 ty(x)=py(x)*COS(a)-pz(x)*SIN(a) 640 tz(x)=py(x)*SIN(a)+pz(x)*COS(a) 650 NEXT:RETURN 660 ' 670 ' Rotation y 680 ' 690 FOR x=1 TO n 700 ux(x)=tx(x)*COS(a)+tz(x)*SIN(a) 710 uy(x)=ty(x) 720 uz(x)=-tx(x)*SIN(a)+tz(x)*COS(a) 730 NEXT:RETURN 740 ' 750 ' Rotation z 760 ' 770 FOR x=1 TO n 780 vx(x)=ux(x)*COS(a)-uy(x)*SIN(a) 790 vy(x)=ux(x)*SIN(a)+uy(x)*COS(a) 800 vz(x)=uz(x) 810 NEXT:RETURN 820 ' 830 ' Routine d'affichage 840 ' 850 RESTORE 940:x=0 860 x=x+1:READ a(x):IF a(x)=255 THEN RETURN ELSE IF a(x)<>0 THEN 860 870 MOVE FNprojx(a(1)),FNprojy(a(1)):FOR i=2 TO x-1:DRAW FNprojx(a(i)),FNprojy(a(i)),1:NEXT:DRAW FNprojx(a(1)),FNprojy(a(1)):x=0:GOTO 860 880 ' 890 ' Data objet 900 ' 910 DATA 100, 100, 100, -100, 100, 100, -100,-100, 100, 100,-100, 100 920 DATA 100, 100,-100, -100, 100,-100, -100,-100,-100, 100,-100,-100 930 DATA 255, 255, 255 940 DATA 1,2,3,4,0, 5,6,7,8,0, 1,5,0, 4,8,0, 2,6,0, 3,7,0, 255
Mise en assembleur
— Basé sur l'article publié dans Quasar CPC numéro 14, Assembleur : Coding, par Zik.
— Enrichi1) par CloudStrife.
 Dans cette section, nous allons voir comment s'y prendre pour réaliser un programme assembleur équivalent au programme BASIC vu ci-dessus. Cependant, le but est d'obtenir des routines rapides moyennant des approximations dans les calculs. La pratique montre que les erreurs dues à ces approximations sont négligeables.
Dans cette section, nous allons voir comment s'y prendre pour réaliser un programme assembleur équivalent au programme BASIC vu ci-dessus. Cependant, le but est d'obtenir des routines rapides moyennant des approximations dans les calculs. La pratique montre que les erreurs dues à ces approximations sont négligeables.
Nous avons vu que la matrice globale de rotation est relativement complexe à calculer et on peut y préférer le calcul successif des trois rotations, comme dans le programme BASIC vu précédemment. Mais une chose importante à voir est que le calcul de cette matrice n'est à faire qu'une seule fois par image (si vous n'avez qu'un objet) et donc le temps mis pour le calcul n'est pas critique. Une fois la matrice prête, vous avez neuf multiplications et six additions par point. Le temps gagné est donc proportionnel au nomre de points de l'objet.
Je reviens une dernière fois sur le calcul de la matrice. Vous avez vu que faire une multiplication avec un Z80 prend du temps, en tout cas beaucoup plus que des additions ou des soustractions. Il existe des formules trigonométriques qui permettent de remplacer les multiplications de sinus et de cosinus par des additions, des soustractions et des divisions par 2. Je vous laisse faire les calculs, on a alors jusqu'à six termes à additionner. Ainsi, le calcul de tous les coefficients de la matrice peut prendre moins de 500µs.
Oh mais que vois-je ? Le petit blond à lunettes a fait les calculs, si si !
En effet 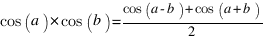 ,
, 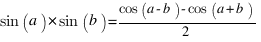 et
et 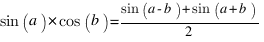
Ce qui nous permet de remplaçer la matrice par celle-ci :
![delim{[}
{matrix{3}{3}
{
{{cos(b - c) + cos(b + c)}/2} {-{sin(c - a) + sin(c + a)}/2+sin(b)*{{sin(a - c) + sin(a + c)}/2}} {{cos(a - c) - cos(a + c)}/2+sin(b)*{{cos(a - c) + cos(a + c)}/2}}
{{sin(c - b) + sin(c + b)}/2} {{cos(a - c) + cos(a + c)}/2+sin(b)*{{cos(a - c) - cos(a + c)}/2}} {-{sin(a - c) + sin(a + c)}/2+sin(b)*{{sin(c - a) + sin(c + a)}/2}}
{-sin(b)} {{sin(a - b) + sin(a + b)}/2} {{cos(a - b) + cos(a + b)}/2}
}}
{]} delim{[}
{matrix{3}{3}
{
{{cos(b - c) + cos(b + c)}/2} {-{sin(c - a) + sin(c + a)}/2+sin(b)*{{sin(a - c) + sin(a + c)}/2}} {{cos(a - c) - cos(a + c)}/2+sin(b)*{{cos(a - c) + cos(a + c)}/2}}
{{sin(c - b) + sin(c + b)}/2} {{cos(a - c) + cos(a + c)}/2+sin(b)*{{cos(a - c) - cos(a + c)}/2}} {-{sin(a - c) + sin(a + c)}/2+sin(b)*{{sin(c - a) + sin(c + a)}/2}}
{-sin(b)} {{sin(a - b) + sin(a + b)}/2} {{cos(a - b) + cos(a + b)}/2}
}}
{]}](http://quasar.cpcscene.net/lib/exe/fetch.php?w=&h=&cache=cache&media=cache_mathplugin%3amath_933_de567917608379445f54ad85aaf9434c.png)
Ah mais voilà, d'accord, il a fait les choses à moitié ! Il reste ne effet que 4 multiplications au lieu des 16 initiales, mais on peut mieux faire en distribuant le 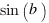 . Et voilà, je dois quand même finir moi même :
. Et voilà, je dois quand même finir moi même :
![delim{[}
{matrix{3}{3}
{
{{cos(b - c) + cos(b + c)}/2} {-{sin(c - a) + sin(c + a)}/2+{cos(b-a+c) - cos(b+a-c) + cos(b-a-c) - cos(b+a+c)}/4} {{cos(a - c) - cos(a + c)}/2+{sin(b-a+c)+sin(b+a-c) + sin(b-a-c)+sin(b+a+c)}/4}
{{sin(c - b) + sin(c + b)}/2} {{cos(a - c) + cos(a + c)}/2+{sin(b-a+c)+sin(b+a-c) - sin(b-a-c)+sin(b+a+c)}/4} {-{sin(a - c) + sin(a + c)}/2+{cos(b-c+a) - cos(b+c-a) + cos(b-c-a) - cos(b+c+a)}/4}
{-sin(b)} {{sin(a - b) + sin(a + b)}/2} {{cos(a - b) + cos(a + b)}/2}
}}
{]} delim{[}
{matrix{3}{3}
{
{{cos(b - c) + cos(b + c)}/2} {-{sin(c - a) + sin(c + a)}/2+{cos(b-a+c) - cos(b+a-c) + cos(b-a-c) - cos(b+a+c)}/4} {{cos(a - c) - cos(a + c)}/2+{sin(b-a+c)+sin(b+a-c) + sin(b-a-c)+sin(b+a+c)}/4}
{{sin(c - b) + sin(c + b)}/2} {{cos(a - c) + cos(a + c)}/2+{sin(b-a+c)+sin(b+a-c) - sin(b-a-c)+sin(b+a+c)}/4} {-{sin(a - c) + sin(a + c)}/2+{cos(b-c+a) - cos(b+c-a) + cos(b-c-a) - cos(b+c+a)}/4}
{-sin(b)} {{sin(a - b) + sin(a + b)}/2} {{cos(a - b) + cos(a + b)}/2}
}}
{]}](http://quasar.cpcscene.net/lib/exe/fetch.php?w=&h=&cache=cache&media=cache_mathplugin%3amath_933_8bf7d02b504f53a42cc896af8886a636.png)
Et oui, vous ne revez pas ! Il n'y a plus une seul multiplication (et si vous regardez attentivement il y a redondance de certains termes, ce qui permet de simplifier encore un peu les calculs)
Les sinus, à dégager !
 Inévitablement (je crois !), si vous voulez faire subir des rotations à votre objet, vous aurez besoin de sinus et de cosinus. À l'instar du Vicks ou du Locabiotal, notre but est de “dégager” les sinus. C'est-à-dire que l'on va avoir recours à une table contenant la valeur du sinus pour chaque angle (elle pourra être calculée grâce au BASIC). Ça nous évitera de faire un long et pénible calcul de série quand on veut le sinus d'un angle.
Inévitablement (je crois !), si vous voulez faire subir des rotations à votre objet, vous aurez besoin de sinus et de cosinus. À l'instar du Vicks ou du Locabiotal, notre but est de “dégager” les sinus. C'est-à-dire que l'on va avoir recours à une table contenant la valeur du sinus pour chaque angle (elle pourra être calculée grâce au BASIC). Ça nous évitera de faire un long et pénible calcul de série quand on veut le sinus d'un angle.
Comme vous le savez, les fonctions sinus et cosinus ne peuvent prendre que des valeurs comprises entre -1 et +1. Ce n'est pas très adapté à l'assembleur qui ne connait que les entiers. Donc on multipliera les valeurs de sinus par une constante avant de les stocker dans la table. Il y a ici un compromis à faire entre précision et temps de traitement. Si votre constante vaut jusqu'à 127, la valeur du sinus pour un angle donné tiendra sur un seul octet. À vous de voir si la précision dans les calculs est suffisante ou s'il faut passer sur 16 bits.
Une optimisation importante peut être obtenue concernant les valeurs des angles. Certains programmeurs s'obstinent à utiliser par exemple le degré comme unité d'angle, avec donc des valeurs de 0 à 359. Du point de vue informatique c'est une unité “quelconque”, comme souvent il est ici très intéressant de considérer les puissances de deux. Si vous prenez des valeurs de 0 à 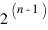 , pour traduire le caractère périodique du sinus, il vous suffira de ne garder que les bits 0 à (n-1) de votre valeur d'angle (un petit
, pour traduire le caractère périodique du sinus, il vous suffira de ne garder que les bits 0 à (n-1) de votre valeur d'angle (un petit AND et le tour est joué).
D'autre part, il n'est pas indispensable d'avoir deux tables (une pour le sinus et l'autre pour le cosinus). On peut trouver le cosinus ) partir du sinus sachant que 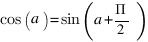 (en radiants !). Là encore, grâce au même
(en radiants !). Là encore, grâce au même AND tout boucle comme il faut !
Plus ou moins...
Tout à l'heure , je vous ai parlé d'un sinus multiplié par une constante. Ceci vous conduit à gérer des valeurs ayant un signe. Comment donc faire en assembleur ?! Nous vous en avons déjà parlé dans d'autres articles, dans ce cas là c'est le bit supérieur de la valeur qui indique le signe (en 8 ou 16 bits pour nous). Il existe d'autres méthodes mais celle que je vous expose est à ma connaissance la plus adaptée au Z80.
Donc, pour un nombre 8 bits, si le bit 7 est à 1, votre valeur est négative. Vous pouvez donc représenter une valeur de -128 à +128 comme suit :
| Binaire signé | Décimal |
|---|---|
01111111 | +127 |
| … | … |
00000001 | +1 |
00000000 | 0 |
11111111 | -1 |
11111110 | -2 |
| … | … |
10000000 | -128 |
Le Z80 possède les instructions NEG et CPL qui permettent de gérer une telle représentation.
On pourra aussi traiter les coordonnées des points en 8 bits signés. Tout au long des calculs, notamment ceux de rotation, il faut faire attention à ce que la notion de signe ne soit pas perdue. Par exemple 127+1 fait -128, il ne faut pas oublier de passer sur 16 bits quand c'est nécessaire.
Méfiez-vous également de la valeur -128 (toujours en 8 bits signés), à cause d'elle l'ensemble [-128,+127] n'est pas symétrique et donc NEG -128 fait -128 !
Vous aurez aussi besoin d'une routine de multiplication. Celle que vous trouverez ici est suffisante à condition d'y ajouter une gestion des nombres négatifs.
L'affichage
Vous pouvez envisager plusieurs types de représentations de votre objet 3D. La plus simple et la plus rapide au niveau de l'affichage (et de l'effaçage) est celle par points. Mais elle ne donne de bons résultats que si l'objet composer au moins une centaine de points ce qui augmente énormément le temps de calcul. On peut compenser en partie ce défaut en choisissant des objets très symétriques et en ne calculant alors les rotations et translations que pour une partie des points.
Pour pouvoir limiter le nombre de points tout en ayant un bon rendu, on peut faire ce qu'on appelle des “vector balls”. Il s'agit en fait d'afficher des sprites au lieu de simples points. Le problème est qu'il ne faut pas afficher ces sprites dans n'importe quel ordre car contrairement à de simples points, ils ont une surface. On a donc à effectuer un tri pour déterminer cet ordre. Un tri selon l'axe z (si l'axe des z est celui perpendiculaire à l'écran) suffit.
Une troisième représentation est celle dite “en fil de fer”. On relie les sommets de l'objet par des segments. On n'a ici pas de tri à faire mais on doit avoir une table disant quels points relier entre eux. Dans une premier temps, vous pouvez utiliser la routine DRAW du système, mais il est plus avantageux d'écrire votre propre routine de tracé de droite. Je vous ai mis ci-dessous un algorithme, il en existe évidemment de nombreuses variantes.
Algorithme de tracé de segment d'après Bresenham :
 ; segment entre (X1,Y1) et (X2,Y2)
; segment entre (X1,Y1) et (X2,Y2)
- X=X1
- Y=Y1
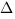 X=abs(X2-X1)
X=abs(X2-X1)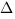 Y=abs(Y2-Y1)
Y=abs(Y2-Y1)- S1=signe(X2-X1)
- S2=signe(Y2-Y1)
- si
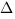 Y>
Y>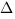 X alors
X alors- tampon=
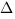 X
X 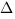 X=
X=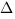 Y
Y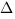 Y=tampon
Y=tampon- XYchange=1
- sinon
- XYchange=0
- fin si
- e=2*
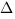 Y-
Y-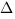 X
X - pour i=1 à
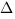 X
X- trace(X,Y)
- tant que e>=0
- si XYchange=1 alors
- X=X+S1
- sinon
- Y=Y+S2
- fin si
- e=e-(2*
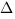 X)
X)
- fin tant que
- si XYchange=1 alors
- Y=Y+S2
- sinon
- X=X+S1
- fin si
- e=e+(2*
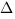 Y)
Y) - fin pour i
- fin
Pour finir, parlons du mode graphique. Le mode 0 est le plus sympathique car il n'a que 2 pixels par octet et il n'y en a que 160×200. Donc le masque est plus simple et il y a moins de pixels à afficher, on gagne donc en rapidité.
Voilà, à vous de mettre en pratique !
Triangles pleins
— Basé sur l'article publié dans Quasar CPC numéro 15, Assembleur : Coding, par Zik.
 Nous allons ici parler de l'affichage de triangles pleins (de manière unie). Et, miracle, vous aurez même droit à un programme d'exemple pratique en BASIC !
Nous allons ici parler de l'affichage de triangles pleins (de manière unie). Et, miracle, vous aurez même droit à un programme d'exemple pratique en BASIC !
J'en vois déjà certains qui se demandent à quoi ça peut bien servir d'afficher des triangles pleins. Eh bien, le but si l'on reste dans le domaine de la 3D, est de représenter des objets dits à “faces pleines” ; c'est-à-dire des objets opaques (ou translucides à la limite). Ceci implique un certain nombre d'opérations supplémentaires par rapport au tracé fil de fer que l'on a déjà vu plus haut. L'affichage, de triangles en l'occurrence, est un point important qui mérite bien d'y consacrer une section complète.
Soit, tout ça fait beaucoup de travail pour notre brave CPC, mais 4 MHz suffisent ; demandez à Face Hugger…
Pourquoi des triangles ?
En fait, le principal intérêt n'est pas d'avoir forcément des triangles mais de ne décrire les objets qu'avec une forme primitive unique. Ainsi, le traitement sera systématique et vous n'aurez à développer des routines que pour cet objet de base.
À partir de là, le triangle s'impose presque : avec un groupe de polygones à trois côtés on peut approcher à peu près n'importe quelle forme globale. Au delà, les triangles ont un grand intérêt si vous voulez déformer votre objet (vu qu'ils ont trois côtés non parallèles). Pour finir, les triangles sont les polygones les plus simples et les routines qui les gèrent sont donc elles aussi plus simples.
Cependant, rien ne vous empêche de choisir comme base des quadrilatères, etc… ou même de ne pas choisir !
Mais comment faire ?
Peu importe la méthode pourvu qu'elle soit rapide avec un minimum de précision. Le nombre d'algorithmes de tracé de triangle est assez élevé, mais la majorité partent du même principe : on ne tracera que les lignes horizontales.
Les lignes horizontales sont celles qui sont les plus rapides à tracer du fait de la structure de l'écran sur CPC. Ce point n'apparait pas vraiment dans le programme BASIC alors qu'en assembleur il est primordial.
À partir du moment où vous avez les coordonnées de départ et d'arrivée pour une ligne donnée, il suffit de faire des tests judicieux pour l'octet de départ du segment et pour celui d'arrivée. La partie intermédiaire n'est alors plus qu'un bête remplissage d'octets identiques.
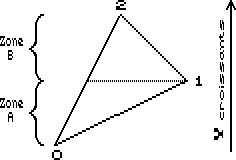
Si on décrit un triangle ligne par ligne, on peut y distinguer deux zones (A et B sur le joli schéma ci-dessous). Elles ont un segment en commun alors que le deuxième diffère.
Donc, dans chaque zone, on se trouve dans des cas similaires et on n'a pas de questions à se poser pendant tout le traitement si ce n'est pour la condition d'arrêt !
Une fois le problème dégrossi, le plus délicat à réaliser est le calcul des abscisses gauche et droite pour chaque ligne. En fait, on n'a pas besoin ici d'un algorithme de droite “complet”. En effet, on n'a besoin que d'une abscisse par ligne représentante de la droite vu que l'on va ensuite remplir
J'espère que ces quelques schémas vous permettront de comprendre mes propos fumeux…
Maintenant que le principe est posé, je vous propose de voir ce que tout cela donne au final grâce au programme BASIC (d'un fort beau gabarit il est vrai) que j'ai fait rien que pour vous (c'est-y pas mignon ?!). Ce programme n'est pas parfait mais donne des résultats très satisfaisants (enfin, moi il me satisfait ; après, ça vous regarde !).
Hibou, un programme !
Parfois, je me dis que je devrais m'abstenir de chercher des titres originaux…
Bref, voyons tout ça dans l'ordre. Après avoir choisi trois points au hasard (que je numérote de 0 à 2), on les classe selon leur coordonnée Y pour avoir la configuration du premier schéma. Le tri se fait selon une variante du tri à bulle.
Dans ce programme, j'ai choisi de commencer à calculer toutes les abscisses pour chaque segment et de les stocker dans des tableaux pour afficher dans un deuxième temps. On aurait tout aussi bien pu calculer au fur et à mesure de l'affichage. Mais si vous voulez transcrire ce programme en assembleur avec cette deuxième façon de procéder, le manque de registres risque d'être pénalisant (quoiqu'avec les registres secondaires…).
La calcul des abscisses est fait par un dérivé de l'algorithme de Bresenham que je vous ai déjà décrit précedemment. Ceci oblige à parcourir tous les points de la droite (le WHILE…WEND est indispensable). On peut donc préférer un algorithme qui se sert directement de l'équation de la droite, mais il faut alors se méfier des erreurs d'arrondi.
Un dernier détail : lors de l'affichage, les lignes sont soit tracées de gauche à droite soit l'inverse. Moyennant quelques tests, on peut s'arranger pour toujours tracer dans le même sens, ce qui simplifie les choses…
La méthode que j'ai adoptée n'est sûrement pas la meilleure, mais j'espère que je vous aurai intéressé et donné des idées pour vos futurs programmes !
Listing : tracé de triangles pleins
(Insérer ici le listing BASIC)