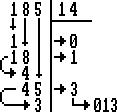Calculer avec le Z80
Nous allons parler ici de tout un tas de méthodes de calculs plus ou moins optimisées, plus ou moins génériques… mais toutes très utiles pour quiconque s'est un jour posé la question des calculs en assembleur Z80.
Calculs arithmétique
— Basé sur l'article publié dans Quasar CPC numéro 13, Assembleur : Software, par Zik.
 Je vais ici tenter de vous parler des opérations mathématiques élémentaires en assembleur. C'est à dire addition, soustraction, multiplication et division. Et hop, c'est parti !
Je vais ici tenter de vous parler des opérations mathématiques élémentaires en assembleur. C'est à dire addition, soustraction, multiplication et division. Et hop, c'est parti !
Additions et soustraction
Commençons par le début. Mis à part INC et DEC que je ne traiterai pas ici, le Z80 possède les instructions ADD et ADC d'une part, SUB et SBC d'autre part. Le C signifie que l'opération implique la carry. ADC réalise une addition avec le paramètre spécifié puis ajoute la carry (qui vaut 0 ou 1) au résultat. SBC soustrait la carry au résultat.
Ces instructions peuvent s'appliquer au registre A (donc en 8 bits) et aux registres HL, IX et IY (donc en 16 bits) avec des restrictions. En effet, SUB n'existe pas en 16 bits, vous êtes donc condamnés à utiliser SBC sans oublier éventuellement de mettre la carry à 0 juste avant (avec OR A par exemple, jetez un oeil ici pour un rappel des bases sur les flags). Ensuite, IX et IY ne connaissent que ADD… Bon, je vous résume tout ça :
- avec A :
ADD,ADC,SBCetSUB- paramètre : (HL), (IX+d), A, B, C, D, E, H, L, n, IXh, IXl (
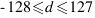 ;
; 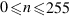 )
)
- avec HL :
ADC,ADDetSBC- paramètre : BC, DE, HL, SP
- avec IX ou IY :
ADD- paramètre BC, DE, IX, SP
Attention, vous ne pouvez pas faire d'addition ou de soustraction entre HL et IX/IY ainsi qu'entre IX et IY.
Dernière remarque : pour les registres 16 bits, vous êtes obligés de passer par un registre comme paramètre.
Causons maintenant un brin des temps machines (je prends le NOP comme unité ) :
ADD/ADC/SUB/SBC A,reg .... 1 ADD/ADC/SUB/SBC A,n ...... 2 ADD/ADC/SUB/SBC A,(HL) ... 2 ADD/ADC/SUB/SBC A,(IX+d) . 5 ADD IX,reg ............... 4 ADD HL,reg ............... 3 ADC HL,reg ............... 4 SBC HL,reg ............... 4
Rotations et décalages
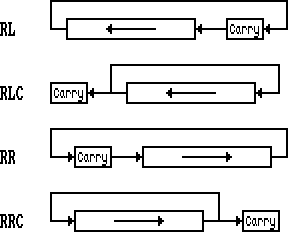
Mieux vaut des schémas qu'un long texte incompréhensible…
Donc les flêches représentent le mouvement des bits de l'octets concerné ; il s'agit soit d'un registre 8 bits (A, B, C, D, E, H, L), soit de (HL), (IX+d) ou (IY+d). Que ce soit pour les rotations ou les décalages, le temps machine pris est de 2 NOP pour les registres, 4 pour (HL) et 7 pour (IX+d) et (IY+d).
 Voici tout d'abord les rotations :
Voici tout d'abord les rotations :
Sachez qu'il existe également les instructions RLA, RLCA, RRA et RRCA qui sont spécifiques à l'accumulateur et qui ne prennent que 1 NOP car elles ne mettent pas à jour les flags autres que la carry.
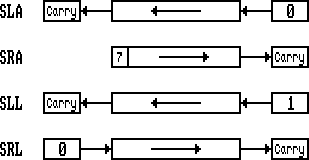
Passons maintenant aux décalages. Avec un petit détail quand même : le 7 du deuxième schéma signifie que le bit 7 ne change pas de valeur.
Il y a donc deux types de décalages, les arithmétiques (SLA, SRA) et les logiques (SLL, SRL). En fait, les premiers sont signés (une valeur 8 bits est considérée comprise entre -128 et +127, le bit 7 étant le signe) et seconds non-signés (valeur de 0 à 255).
 Dernière chose avant de passer au paragraphe suivant : l'instruction
Dernière chose avant de passer au paragraphe suivant : l'instruction SLL est dite “non-documentée” ; c'est-à-dire qu'elle n'est pas connue de la plupart des assembleurs. Donc, dans mon extrême bonté, je vous donne les codes machine qui lui correspondent :
&CB &30 .......... SLL B &CB &31 .......... SLL C &CB &32 .......... SLL D &CB &33 .......... SLL E &CB &34 .......... SLL H &CB &35 .......... SLL L &CB &36 .......... SLL (HL) &CB &37 .......... SLL A &DD &CB &dd &36 .. SLL (IX+&dd) &FD &CB &dd &36 .. SLL (IY+&dd)
Multiplions !!
On peut distinguer ici deux familles de multiplications : les sympathiques et les autres (j'ai failli dire une grossièreté). Pour illustrer mes propos (fumeux), à partir de maintenant je vais me rapporter presque systématiquement à la base 10 que vous connaissez bien.
Qu'est-ce qui vous parait le plus facile comme multiplication dans notre chère base 10 ? Ben, la multiplication par 10 (celui qui a dit par 2 viendra me voir à la fin du cours). Eh bien, en base 2 (en binaire), celle qui nous intéresse, c'est bien multiplier par 2 qui est le plus simple : il suffit de faire un décalage d'un bit vers la gauche et le tour est joué.
Bon, il ne faut quand même pas oublier que faire 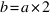 c'est pareil que
c'est pareil que 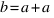 . Donc le plus rapide pour multiplier A par une puissance de 2 est une succession de
. Donc le plus rapide pour multiplier A par une puissance de 2 est une succession de ADD A,A et pour HL de ADD HL,HL. En revanche, pour multiplier DE par 2, vous devrez faire un truc du genre SLA E suivi d'un judicieux RL D.
 Vous l'avez compris (je vous admire), l'assembleur Z80 n'ayant pas d'instruction de multiplication, il faut bidouiller avec les additions et les décalages et rotations. Ainsi, pour multiplier par 3, on fera
Vous l'avez compris (je vous admire), l'assembleur Z80 n'ayant pas d'instruction de multiplication, il faut bidouiller avec les additions et les décalages et rotations. Ainsi, pour multiplier par 3, on fera 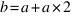 et on doit donc passer par un registre supplémentaire.
et on doit donc passer par un registre supplémentaire.
; A=A*3 ld c,a add a,a add a,c
Il peut arriver également que l'on ait à multiplier deux registres entre eux.
Voici un programme qui multiplie DE par A :
; HL=DE*A ld b,8 ld hl,0 Boucle rra jr nc,saut add hl,de Saut sla e rl d djnz boucle
Attention, le résultat est dans HL et donc sur 16 bits, il est donc possible d'avoir un débordement lors de la multiplication.
Au niveau du principe : on décompose bit à bit le registre A en commençant par celui qui a le poids le plus faible. Si le bit est mis, on ajoute DE à HL ; dans tous les cas, on multiplie DE par 2 afin de le mettre en correspondance avec le prochain bit de A qui sera testé. Je suis pas sûr d'être clair sur ce coup là !
C'est comme quand on pose une multiplication (la fameuse base 10 !)… Bon, passons à la suite…
La division
 Ici aussi, les divisions par les puissances de 2 sont avantageuses : il suffit de faire un décalage vers la droite par un
Ici aussi, les divisions par les puissances de 2 sont avantageuses : il suffit de faire un décalage vers la droite par un SRL par exemple pour diviser par deux.
Avant de continuer je vais vous faire un petit rappel de vocabulaire sur les éléments d'une division, ça me simplifiera la tâche :
En ce qui concerne la division par un nombre quelconque, il y a bien la méthode qui consiste à retrancher le diviseur du dividende jusqu'à ce que celui-ci déborde en comptant le nombre de soustractions… mais c'est une méthode médiocre car elle prend un temps machine très variable et qui peut être très important.
En fait, la meilleure méthode (enfin je pense) est celle que vous avez l'habitude d'appliquer en posant une division. Petits schémas !
On prend d'abord le chiffre de gauche du dividende, on essaie d'y retrancher le diviseur. Si on dit que X est le nombre de fois que le diviseur “entre” dans le dividende, on lui soustrait X*diviseur. Puis on abaisse le chiffre suivant. Ainsi de suite jusqu'aux unités.
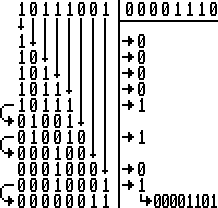
En binaire, c'est exactement la même chose. La subtilité vient du fait que tout à l'heure X pouvait avoir toutes les valeurs de 0 à 9 mais ici on n'a que 2 cas : 0 ou 1. Regardez la routine ci-dessous : on récupère les bits de E en commençant par le 7, on le récupère dans A et on voit si A<D. Si oui, on va à Saut sans soustraire… pour le reste, vous devriez comprendre seuls.
; C=E/D ; A=Reste ld b,8 xor a ld c,a Boucle sla e rla cp d jr c,saut sub d Saut ccf rl c djnz boucle
Calcul à base de tables
— Basé sur l'article publié dans Quasar CPC numéro 19, Assembleur : Coding, par Zik.
Dans tout programme conséquent, on est amené à effectuer des calculs. Selon le cas, les routines de calcul sont plus ou moins faciles à mettre au point et leur temps d'exécution est critique ou non. Lorsque l'on peut se permettre de “sacrifier” un peu (ou beaucoup) d'espace mémoire, on a alors souvent recours à l'utilisation de tables de valeurs. C'est le thème de cette section.
Quoi ? Comment ?
Évidemment, à partir du moment où l'on décide d'utiliser un tableau, plusieurs questions se posent. Il faut choisir le format des valeurs qu'il contiendra, la place mémoire que l'on peut lui allouer et la manière la plus judicieuse pour agencer ses données. Je vous propose maintenant de voir cela plus concrètement sur des exemples.
Premier exemple
Imaginez que vous voulez réécrire le PLOT du BASIC pour l'adapter à votre application ; c'est-à-dire que vous souhaitez afficher un pixel à l'écran à partir de ses coordonnées. Vous devez donc vous débrouiller pour obtenir l'adresse à laquelle vous devrez écrire l'octet adéquat (comme Sheila). Je vais m'intéresser ici seulement au calcul de l'adresse de l'octet de début de ligne (à gauche de l'écran).
Voici le repère associé à l'écran :
On souhaite obtenir l'adresse de l'octet de coordonnées (0,y). Du fait de la structure de la mémoire vidéo du CPC, le calcul est le suivant :
- On a :
adr=largeur*y/8 + (y AND 7)*&800 - Soit :
adr=80*y/8 + (y AND 7)*&800 - Soit :
adr=10*y + (y AND 7)*8*256 - Soit enfin :
adr=(8+2)*y + (y AND 7)*8*256
largeur est la largeur en octets (axe x) de l'écran.
Je prends pour largeur la valeur standard qui est 80. Si on décrit ce calcul en assembleur, voilà ce que ça peut donner :
; l = Coordonnée y Calcul ld a,l ld h,0 add hl,hl ; hl=y*2 ld d,h ld e,l ; de=hl=y*2 add hl,hl ; hl=y*4 add hl,hl ; hl=y*8 add hl,de ; hl=y*8+y*2=y*10 and 7 ; a=y AND 7 add a,a ; a=(y AND 7)*2 add a,a ; a=(y AND 7)*4 add a,a ; a=(y AND 7)*8 ld e,0 ld d,a ; de=a*256 add hl,de ; hl=résultat
C'est pas si mal ; le calcul prend 28µs. Celà dit, il faut encore ajuster le résultat si l'écran n'est pas situé à l'adresse &0000. Mais on se doute bien que l'on peut faire plus rapide grâce à une table précalculée. Et en effet, si on stocke les adresses de début de ligne dans l'ordre, de la ligne 0 à 255 maximum, il est facile d'aller les récupérer en fonction d'un paramètre.
On a quand même recours ici à une astuce souvent très avantageuse pour les tables, il s'agit de la placer à une adresse mémoire de la forme &XX00 (c'est-à-dire dont l'octet de poids faible est nul). Ceci évite des opérations coûteuses en temps machine.
; l = Coordonnée y Calcul xor a ; a=0 ; carry=0 rl l ; l=l*2 adc a,table/256 ld h,a ld a,(hl) ; hl=adresse paire inc l ; donc "inc l" suffit ld h,(hl) ld l,a ; hl=résultat ... org &xx00 Table dw &C000 dw &C800 ...
Cette routine nécessite une table de 512 octets mais on obtient le résultat cette fois en seulement 12µs. Le temps de calcul a donc été sensiblement diminué. Je précise un détail sur le programme : table/256 est calculé lors de l'assemblage et a comme valeur le poids fort de l'adresse à laquelle est stockée la table.
Là où du temps se perd dans la routine précédente, c'est lors de la multiplication par 2 de L qui permet de déduire l'adresse de la table où se trouve la valeur qui nous intéresse. Cette multiplication est dûe à la taille des éléments de notre table qui sont des valeurs 16 bits et qui occupent donc deux octets. Pour s'en débarasser, il faut donc découper la table de words en deux d'octets.
C'est alors que j'introduis la dernière routine de ce premier exemple :
; l = Coordonnée y Calcul ld h,table/256 ld a,(hl) inc h ld h,(hl) ld l,a ; hl=résultat ... org &4500 ; adresse en &XX00 Table db &00 ; poids faibles db &00 ... org &4600 ; =&4500+&100 db &C0 ; poids forts db &C8 ....
Les deux tables sont toujours placées à des adresses de poids faible nul et elles sont distantes de 256 octets (&100). La première table contient les poids faibles des éléments de la table et la deuxième les poids forts. Ainsi, un simple LD permet de trouver l'adresse de poids faible et un simple INC H passe aux poids forts ! La routine ne prend plus que 8µs pour le même résultat, comme quoi, ça vaut le coup de chercher un peu !
Deuxième exemple : trigonométrie
Oui, vous avez bien lu. Si vous lorgnez du côté des articles consacrés aux calculs 3D, vous trouverez tout un tas de jolies formules comportant parfois des sinus et des cosinus. Eh bien, si vous comptez faire de la “3D temps-réel”, comme ont dit, vous avez plus besoin de vitesse que de précision ; l'utilisation des tables est toute indiquée.
 Avant de foncer tête baissée, intéressons-nous aux spécificités des fonctions sinus et cosinus. Déjà, elles peuvent prendre des valeurs positives ou négatives réelles, ce qui nous déplaît plutôt. Ensuite, elles sont périodiques et le cosinus peut être déduit du sinus simplement. Pour finir, les valeurs prises sont réelles mais bornées, on sait en effet que les fonctions sinus et cosinus ne retournent que des valeurs comprises entre -1 et +1, ensemble symétrique par rapport à 0.
Avant de foncer tête baissée, intéressons-nous aux spécificités des fonctions sinus et cosinus. Déjà, elles peuvent prendre des valeurs positives ou négatives réelles, ce qui nous déplaît plutôt. Ensuite, elles sont périodiques et le cosinus peut être déduit du sinus simplement. Pour finir, les valeurs prises sont réelles mais bornées, on sait en effet que les fonctions sinus et cosinus ne retournent que des valeurs comprises entre -1 et +1, ensemble symétrique par rapport à 0.
La suite dépend de la précision nécessaire à vos calculs. La table sera la valeur du sinus sur toute une période pour chaque valeur d'angle. Certes, on pourrait reconstituer le sinus complet à partir d'un quart ou d'une demi-période mais cela demanderait des opérations supplémentaires. Je propose de stocker chaque valeur de sinus sur seulement un octet, en binaire signé (aussi appelé complément à 2). Donc, on place finalement dans la table la valeur de 127*sinus(angle), tant pis pour la valeur -128, restons sur un intervalle symétrique. Si vous souhaitez une précision plus grande, vous pouvez allouer deux octets, vous vous retrouvez alors dans le cas du premier exemple.
La valeur de sinus(angle) est réelle mais l'angle lui aussi est réel. Dans beaucoup de cas, une précision au degré est amplement suffisante. Mais si l'on pense au programme, il est nettement plus intéressant de choisir une puissance de 2 au lieu de 360… et je pense en particulier à 256. Le nombre 256 est miraculeux dans ce cas, car il permet de traduire sans effort le caractère périodique des fonctions périodiques telles que le sinus. Démonstration :
- en radians :
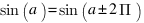 ,
, - avec notre choix d'angle :
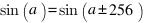 1).
1).
Quand on va ajouter, soustraire, multiplier… bref, faire des calculs 8 bits sur les angles, le modulo 256 va se faire naturellement ; on n'aura plus qu'à aller chercher la valeur du sinus parmi nos 256 octets sans se poser plus de questions. Au niveau assembleur, on prendra soin de placer la table sur une adresse de poids faible nul et le code résultant est alors ridiculement simple :
; l = angle Calcul ld h,table/256 ld a,(hl) ; a = résultat ... org &XX00 Table ds 256 ; table de sinus
Pour ce qui est du cosinus, comme on l'a déjà dit, on peut le déduire de la table de sinus :
- en radians :
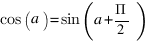 ,
, - avec notre choix d'angle :
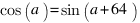 .
.
Il suffit donc d'ajouter 64 à l'angle et d'appeler la même routine que précédemment pour obtenir le cosinus.
Conclusion
Un dernier mot avant de terminer cette section. Il vous faut à un moment donné générer les tables, le BASIC s'y prête bien ; vous pouvez calculer la table à une adresse convenue ou générer un morceau de source assembleur (en ASCII pour Maxam) à inclure dans le source principal. Vous pouvez aussi générer la table en assembleur en utilisant les vecteurs mathématiques du système… ou pas !