— Basé sur les articles publiés dans Quasar CPC numéro 16 et numéro 17, Dossier, par Zik.

— Il serait intéressant d'ajouter une section expliquant comment contrètement jouer des samples sur CPC avec le PSG.

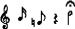Notre oreille est sensible aux ondes sonores qui se propagent dans l'air. Ce sont en fait des vibrations se déplaçant à environ 340m/s dans l'air. Cela dit, le son peut aussi exister dans d'autres milieux. Il se propage par exemple à 1425m/s dans l'eau et à 5000m/s dans l'acier.

Un son est essentiellement caractérisé par sa fréquence, son intensité et son timbre.

La fréquence détermine la hauteur du son. Elle est le nombre de vibrations par seconde, son unité est le Hertz (Hz). L'oreille humaine perçoit les sons entre 15 et 20000Hz (en fait ça dépend de votre age). Plus la fréquence est grande, plus le son est haut (ou aigu). Vous savez peut-être que le LA de référence est à 440Hz, et bien si vous doublez la fréquence, vous obtenez encore un LA (à 880Hz) une octave au dessus. Je reviendrai sur ces considérations musicales un peu plus bas.

La variation périodique de la fréquence d'une note autour d'une valeur moyenne est appelée vibrato.

L'intensité est le deuxième paramètre d'un son, il correspond à l'amplitude des vibrations sonores. On a l'habitude de l'exprimer en décibel (dB). Le rapport entre l'amplitude et le décibel n'est pas linéaire mais logarithmique. La zone audible s'étend de 1 à 120dB, au delà l'oreille souffre et peut subir des lésions.

On peut remarquer que l'intensité dépend de la distance à l'émetteur ainsi que de la fréquence. Nous n'entendons en effet pas toutes les fréquences avec la même intensité. Nous percevons plus difficilement les sons hauts et bas que les sons de fréquence moyenne (de 1000 à 3000Hz). C'est dans cette zone fréquentielle que se situent les vibrations typiques de la voix humaine.

L'intensité d'un son évolue toujours dans le temps (elle diminue généralement). Si elle oscille périoquement, on appelle cela un trémolo.

Le troisième paramètre est le plus complexe. Le timbre permet de reconnaitre la nature d'un son. Plusieurs instruments différents peuvent jouer la même note et on réussira quand même à les dissocier; cela parce qu'un hautbois (au hasard !) n'a pas le même timbre qu'une flûte, etc.. C'est en fait le format de la vibration (de l'onde) qui définit le timbre.

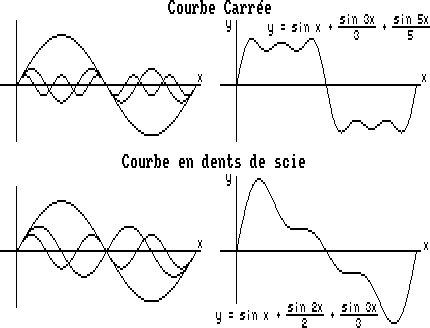
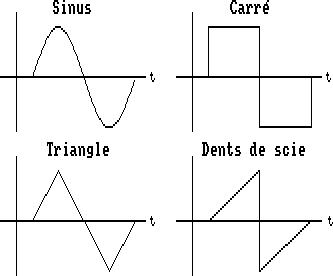Considérons par exemple les quatre formes d'ondes de la figure 1. Chacun a un timbre différent, le sinus est doux, le triangle un peu plus nasillard et le carré assez brut.

On peut dire finalement que le timbre est directement dépendant du spectre fréquentiel du son; si vous ne savez pas ce que cela signifie, jetez donc un coup d'œil à la figure 2.

On peut décomposer une forme d'onde en somme de sinus multiples par des coefficients. C'est ce que l'on appelle décomposition en série de Fourier. Le schéma ci-dessus vous montre ce que cela donne pour un signal carré ou en dents de scie. On n'a représenté que trois sinusoïdes mais le développement complet va théoriquement jusqu'à l'infini. Je ne vais pas rentrer plus dans les détails.

Un spectre représente, pour chaque fréquence de sinusoïde du développement, l'amplitude associée (qui est proportionnelle au coefficient du sinus correspondant). Par exemple, pour le signal carré du schéma, on a une composante d'amplitude 1 pour la fréquence fondamentale, une deuxième composante au triple de cette fréquence et d'amplitude 1/3 seulement cette fois-ci et ainsi de suite. Plus vous ajoutez de termes plus leur somme se rapproche de la forme d'onde réelle et plus le spectre se complète.

La fréquence la plus basse d'un son s'appelle, comme je l'ai déjà dit, fréquence fondamentale ; elle correspond généralement à la note du son. Les autres fréquences présentes dans le spectre sont des harmoniques. Le timbre d'un son dépend du nombre d'harmoniques et de leurs rapports fréquentiels et d'amplitude.

La vision d'une onde sous la forme de son spectre est particulièrement intéressante car elle permet de savoir quelle plage de fréquence il faut au minimum pouvoir reproduire (après un enregistrement) pour garder ses principales caractéristiques. De plus, l'oreille humaine ne réagit qu'à des vibrations sinusoïdales.

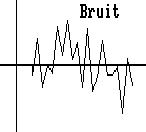
Un type de son particulier est le bruit. C'est en fait plutôt un mélange de sons sans périodicité marquée et donc sans note identifiable. On qualifie typiquement de bruit le souffle qui est émis par des haut-parleurs en l'absence de signal utile.

Il existe divers procédés pour enregistrer des sons et de la musique. On y distingue deux grandes familles qui sont l'enregistrement directement en analogique et le stockage sous forme numérique. Dans les deux cas, on est obligé de faire de l'échantillonngage. C'est-à-dire de découper le signal en fenêtres temporelles (de longueur généralement constante) et de prendre un échantillon représentatif du signal par fenêtre. Si ce découpage n'est pas fait explicitement, il réside dans le procédé de stockage lui-même, au niveau physique. Par exemple, pour le stockage analogique, sur une cassette audio la limite est en partie dûe à la densité de particules magnétiques sur la bande. Pour un disque vinyle c'est au niveau de la précision de gravure et du saphir qu'est la limitation.

Le problème des enregistrements analogiques est leur usure probable. Un échantillon peut très bien voir sa “valeur” se modifier. Il n'y a pas de moyen de corriger cette dérive. Par contre, en numérique, un des points de départ est de ne stocker physiquement que deux niveau (0 ou 1). La “distance” entre ces deux niveaux est telle que l'usure du support a très peu de chances (dans des conditions d'utilisation normales !) de changer un 1 en 0 ou inversement. L'inconvénient est qu'il faut utiliser une suite de tels niveaux pour représenter un échantillon stocké en analogique. Donc, le volume de données est plus élevé en numérique mais on y gagne en fiabilité et aussi on peut confier les valeurs numériques à des circuits logiques et microprocesseurs. Rien n'empêche donc alors d'appliquer des algorithmes de compression de données !

Je devrais peut-être plutôt dire digitalisation… Cela consiste à donner une représentation numérique d'un signal. Certaines règles sont à respecter pour obtenir un résultat fidèle.

Les sons que nous voulons stocker dans la mémoire de l'ordinateur sont, à la base, analogiques. Comprenez par là qu'ils peuvent prendre n'importe quelle valeur d'amplitude parmi une infinité. Une telle valeur est impossible à stocker ; il va falloir dégrader le signal afin de passer d'un ensemble infini de valeurs à un nouveau de taille finie. Le principe est simple non ?

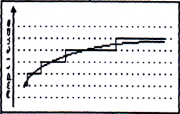
La première dégradation du son par l'échantillonnage est donc une discrétisation de l'amplitude. C'est ce que vous montre vaguement la figure 3, les lignes horizontales en pointillés montrent les valeurs possibles du signal échantillonné (la fonction en escaliers) alors que le signal continu est celui de départ.

Il est évident que plus on aura de valeurs possibles, meilleure sera l'approximation. Avec une résolution de 8 bits, on a 256 niveaux, l'erreur de quantification maximale est 1/256ème de la valeur digitalisée. Cette erreur est tout à fait acceptable mais en Hi-Fi on est plus exigent sur la résolution et les échantillons sont au moins sur 16 bits.

Remarquez cependant que l'erreur de quantification augmente si on n'utilise pas la pleine échelle des valeurs disponibles. Pour avoir une qualité optimale il faut amplifier analogiquement le signal de façon à couvrir au mieux 256 valeurs possible en 8 bits lors de l'échantillonnage.

Mais la digitalisation comporte un autre paramètre important qui est…

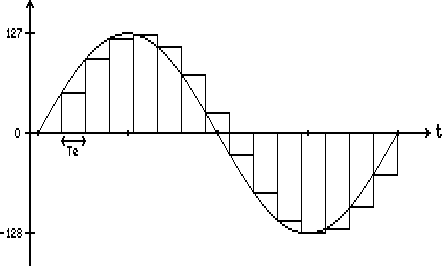
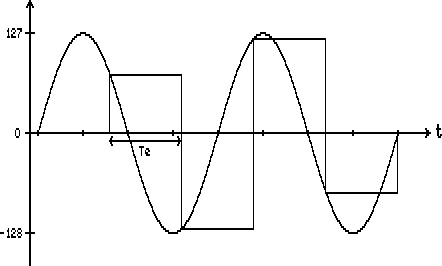
Il exprime le nombre d'échantillons du signal que l'on prélève par seconde. On parle aussi de fréquence d'échantillonnage (Fe). Plus elle est élevée meilleure sera la restitution. Regardez à ce propos les jolies figures 4 et 5. L'échelle des temps de la deuxième est deux fois plus condensée que l'autre. Te est la période d'échantilonnage (égale à 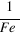), elle est beaucoup plus grande sur la figure 5. En conséquence, la fonction échantillonnée (toujours celle en escaliers) n'est plus vraiment représentative du signal de départ.

J'ai omis de vous dire que l'on ne peut évidemment définir Fe que si l'on échantillonne à interface de temps régulier, ce qui est généralement le cas. Mais on pourrait imaginer un système dynamique où l'on échantillonne d'autant plus fréquemment que le signal varie rapidement.

En tout cas, on se rend bien compte qu'il faut choisir Fe en tenant compte de la fréquence la plus élevée du spectre du signal à digitaliser. Il faut que Fe soit au moins deux fois supérieure à celle-ci, c'est entre autre ce que dit le théorème de Shannon. Si la qualité “CD” spécifie un Fe de 44100Hz, c'est pour pouvoir reproduire les harmoniques jusqu'à environ 22kHz, ce qui couvre tout le spectre audible par notre oreille.

On peut cela dit faire une critique. Si l'on a un Fe double de la fréquence de la plus haute harmonique, alors on se retrouve dans un cas pire que celui de la figure 3. Deux échantillons seulement représentent cette fréquence, donc ce que l'on reproduit est en fait un signal carré dont l'intensité est atténuée par rapport à celle de l'harmonique considérée. Or, je vous ai déjà dit dans une section précédente qu'un son carré n'a pas le même timbre qu'un sinus. Eh bien ce n'est pas très grave si la fréquence en question est assez aiguë (!). En effet, nous avons d'autant plus de mal à discerner le timbre que la fréquence est rapide.

De plus, Fe ne sera pas exactement égale au double de la fréquence de la plus haute harmonique. En conséquence la prise d'échantillon correspondra pour chaque période à un instant différent du signal (je parle toujours de la plus haute harmonique). Donc, sur plusieurs périodes certes, le signal sera donc intégralement reconstitué.

Je sens bien que tout le monde n'a pas compris ce que je viens d'écrire. Pour vous aider, je dirais que c'est un peu comme de la digitalisation en mode multipasse… vous faites ce que vous voulez de cette comparaison !

Vous pouvez digitaliser une musique complète ou alors simplement une note jouée par un instrument. Dans ce dernier cas, il est intéressant de savoir générer n'importe quelle note à partir d'une seule échantillonnée.

Une note est, à quelques chose près, un signal périodique. C'est-à-dire que le même motif se répète régulièrement, souvent en s'atténuant. Le nombre de répétitions de ce motif par seconde est la fréquence du son. Elle correspond à la plus basse fréquence du spectre du son. On a la formule suivante :

Où 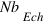est le nombre d'échantillons qui reproduisent le motif.

Par exemple, sur la figure 4, .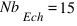

Le LA de référence a une fréquence de 440Hz (le motif est répété 440 fois chaque seconde). Si on double la fréquence on tombe sur la même note, mais une octave plus haut (plus aiguë). Il faut par ailleurs savoir que notre gamme comporte 12 notes par octave. Ces notes sont :

Do → Do# → Ré → Ré# → Mi → Fa → Fa# → Sol → Sol# → La → La# → Si

Deux notes consécutives de cette énumération sont espacées (en hauteur) d'un demi-ton. Le dièse (#) augmente la hauteur d'un demi-ton contrairement au bémol (b) qui abaisse la note. Vous pouvez remarquer qu'il n'y a qu'un demi-ton entre Mi/Fa et Si/Do.

La fréquence de la note située un demi-ton au dessus est obtenue en multipliant par le coefficient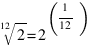

Donc, en partant du LA :

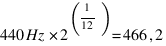(LA#)

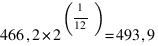(SI)

Remarque :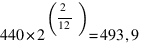

Si vous voulez jouer maintenant une note quelconque à partir par exemple du LA que vous avez digitalisé, vous avez deux solutions :

• soit vous envoyez tout le temps les échantillons à une vitesse fonction de la note que vous souhaitez jouer,
• soit vous envoyez des échantillons à une fréquence fixe mais en sautant ou dupliquant certains valeurs.

La première méthode a l'avantage de ne pas dégrader la forme d'onde comme le fait la deuxième. Mais voici un exemple. Vous avez échantillonné le signal de la figure 4 à 6600Hz, c'est donc un LA 440. Vous voulez ensuite reproduire un DO 3 demi-tons au dessus, il faut donc rejouer à 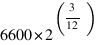ce qui fait environ 7849Hz. Avec le hardware donc le CPC dispose cela signifie que plus on jouera une note aiguë plus cela prendra de temps machine. Le hardware nous impose aussi d'utiliser la deuxième méthode quand on souhaite faire de la polyphonie.